Eclipse Technologies

The basis of the Copernican Principle is that the location in the universe at which we currently exist is not unique. This is the concept Copernicus used to arrive at his discovery that the Earth is not the center of the Universe, as was previously believed. Today, I’d like to explore its potential for use in markets.

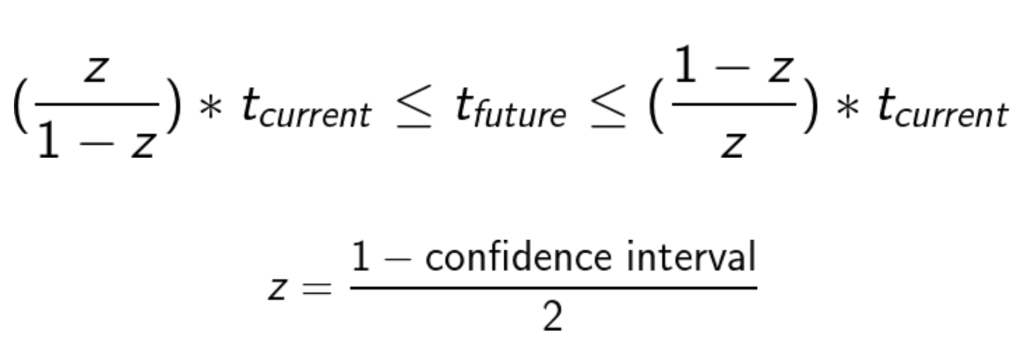
The Copernican Principle can be applied not only to location but also to time. That is, we assume the moment at which we are observing something is not unique. Using this assumption, we can predict the lifetime of any phenomenon using the Copernican Lifetime Equation pictured below.

*tcurrent is the amount of time something has existed for, tfuture is the expected amount of time it will exist for, and confidence interval is the measure of how confident we are in this prediction.

The easiest “out-of-box” way to implement this concept in a strategy would be to use the Copernican Lifetime Equation (CLE) to make predictions on the duration of trends in asset prices. We can create confidence intervals to predict the lifetime of trends given the amount of time they have existed for.

A quick visualization of the premise behind CLE:

Here’s an example. Let’s image we’ve just opened up a chart of SPY and observed a period of consolidation that has existed for 13 days. If we assume that we aren’t observing the consolidation during the first or last 2.5% of its lifetime, we can use the equation above to predict its full length (assuming a 95% confidence interval). After plugging in the numbers, we find that on average, 95% of consolidation periods that have lasted 13 days have a “lifetime” of between 1/3 of a day and 507 days. So, a fairly broad estimate that is practically speaking, useless.

This doesn’t bode well for our hopes of building a strategy around the CLE. How might we go about trying to profit off of our predictions?

Well, we can try a few things. First we’d decrease our level of confidence in order to get a more accurate prediction. This is allowable if we choose the right instrument to trade, such as options, that give us a high risk to reward ratio, so that over the long run our trades can have a positive expected value even with a low probability of an accurate prediction.